INTRODUCCIÓN
Actualmente, las matemáticas se consideran una disciplina compleja y poco atractiva, lo que disminuye la motivación estudiantil y afecta negativamente el rendimiento académico. En la educación básica media, los estudiantes enfrentan dificultades para participar y mantener el interés en el aprendizaje de esta asignatura. La motivación resulta esencial; como señala Mora et al. (2024), y dentro del aula es un factor determinante para el éxito del proceso de enseñanza-aprendizaje. Estas dificultades pueden originarse por varios motivos: la visión de la materia como algo abstracto, la ausencia de conexiones con situaciones diarias y la utilización de métodos tradicionales que no promuevan la participación activa.
Las teorías del aprendizaje tienen como objetivo potenciar la enseñanza para beneficio de la educación. En este sentido, la teoría sociocultural de Vigotsky, la autodeterminación de Deci y Ryan y el aprendizaje significativo de Ausubel constituyen referentes para aplicar estrategias didácticas basadas en contenidos contextualizados, trabajo colaborativo, gamificación y retroalimentación personalizada en lógica matemática (Alt, 2023; Mafarja et al., 2023; Taufikurrahman et al., 2021).
La teoría de la autodeterminación plantea una gestión entre motivación intrínseca y extrínseca (Donald, 2025). La primera se asocia al interés y disfrute natural de la actividad; las segunda, a beneficios externos como notas o reconocimientos. Promover la motivación intrínseca fomenta el compromiso, el interés y la constancia. Según Hernández (2023), la motivación autónoma se nutre de tres necesidades psíquicas: autonomía (actuar por decisión propia aun siguiendo indicaciones externas), relación (vínculos sociales equilibrados que favorezcan integración y bienestar) y competencia (percepción personal de la propia capacidad).
Para Ausubel, citado por López de Aguilera & Soler (2021), el aprendizaje es más eficaz cuando los nuevos contenidos se relacionan con conocimientos previos. En lógica matemática, esto implica que los estudiantes cuenten con bases sólidas para comprender y asimilar conceptos más complejos.
Por su parte, la teoría sociocultural de Vigotsky sostiene que el aprendizaje se construye mediante la interacción con otras personas en contextos sociales y culturales, siendo el lenguaje un instrumento esencial. Como lo afirma Velásquez et al. (2023), una formación adecuada incrementa la interacción social y seguridad para expresarse. Un elemento central en esta teoría es la zona de desarrollo próximo, que se refiere al potencial de aprendizaje cuando el estudiante recibe apoyo de alguien con mayor experiencia.
En matemáticas, el acompañamiento al estudiante facilita la comprensión y el desarrollo del pensamiento lógico (Cerón & Marrero, 2024). Macías & Zambrano (2023) recomiendan estrategias didácticas basadas en contenidos contextualizados, trabajo colaborativo, clases gamificadas que no requieren necesariamente tecnología y retroalimentación personalizada para mejorar la comprensión matemática.
En este sentido, Núñez et al. (2020) afirman que el profesorado debe motivar y generar pensamiento crítico con la aplicación de las estrategias adecuadas. Un docente formado no solo domina contenidos, sino que sabe adaptarlos a su grupo. Peña (2024) destaca que es fundamental seleccionar estrategias significativas acordes al tema y a las necesidades cognitivas de los estudiantes para garantizar el proceso de aprendizaje.
Por otra parte, la familia también cumple un papel esencial, al ser el primer espacio de aprendizaje y socialización. Según Bazán et al. (2021), la relación familia-estudiante es un factor clave para el desarrollo académico, el compromiso e iniciativa educativa surgen de forma espontánea y no solo como respuesta a exigencias escolares. Rodríguez (2023) agrega que las expectativas familiares sobre el rendimiento son un indicador relevante de los logros escolares. Adicionalmente, Morales et al. (2024) señalan que el nivel socioeconómico influye en el rendimiento escolar. En el caso de los hogares con menores ingresos generalmente tienen menos recursos didácticos, apoyo en casa y oportunidades de aprendizaje enriquecedoras, lo que repercute directamente en el progreso educativo.
Además, en la enseñanza tradicional, la práctica de ejercicios repetitivos, memorización y ausencia de ejemplos prácticos y contextos reales predominan, lo que restringe la comprensión profunda y disminuye la motivación (Valero & González, 2021). Otro factor es la ansiedad matemática, potenciada por expectativas externas, presión evaluativa y baja percepción de autoeficacia, lo que genera actitudes desfavorables hacia el aprendizaje (Nerio & Ramírez, 2024).
El INEVAL (2023-2024), a través de la evaluación “Ser estudiante”, identificó que en Básica Media persisten dificultades para alcanzar los aprendizajes esperados en matemáticas, evidenciando una brecha compleja entre los objetivos curriculares y los resultados obtenidos. En este escenario, Ruiz & Reyes (2025) señalan que los estudiantes no adquieren las habilidades lógico-matemáticas necesarias por falta de estrategias didácticas, y destacan la importancia de la formación continua del docente para implementar métodos adecuados a su grupo.
Por tanto, en la educación básica media en Ecuador, la enseñanza de las matemáticas se enfrenta a un escenario complejo que se encuentra marcado por: bajos niveles de motivación estudiantil, escasa conexión de los contenidos con la vida cotidiana, y persistencia de métodos tradicionales centrados en la repetición mecánica. Los factores analizados limitan la participación de los alumnos y genera actitudes desfavorables hacia el aprendizaje, repercutiendo en el desarrollo del pensamiento lógico-matemático.
En la Unidad Educativa Réplica Nicolás Infante Díaz, a pesar de los esfuerzos de los docentes en la planificación de actividades y la relación de los contenidos matemáticos a la vida cotidiana, se observa poca incorporación de metodologías innovadoras como la gamificación o el trabajo colaborativo estructurado. Adicionalmente, se identifican un grupo de limitaciones en las teorías pedagógicas contemporáneas, lo que restringe la capacidad de la diversificación de estrategias y la motivación a los estudiantes en la enseñanza de las matemáticas. La situación problemática descrita con anterioridad incide directamente en el desarrollo del pensamiento lógico-matemático de los estudiantes de básica media, generando la necesidad de repensar las prácticas docentes y fortalecer la capacitación pedagógica orientada hacia la innovación educativa.
Por ello, el objetivo del trabajo es analizar la aplicación de estrategias didácticas en la enseñanza de las matemáticas para el fortalecimiento del pensamiento lógico-matemático en la Unidad Educativa Réplicas Nicolás Infante Díaz.
MÉTODOS
Esta investigación se fundamenta en un enfoque mixto que combina técnicas cuantitativas y cualitativas para abordar el problema desde diversas perspectivas. Este enfoque permite una comprensión más integral y profunda al integrar datos numéricos con experiencias y percepciones de participantes.
El diseño del estudio es descriptivo-exploratorio, no experimental, ya que se busca examinar las características del fenómeno en su contexto real sin manipular variables. Este diseño facilita identificar cómo se aplican y perciben las estrategias didácticas en la enseñanza del razonamiento lógico-matemático dentro de la Unidad Educativa Réplicas Nicolás Infante Díaz. Asimismo, se adoptó el método inductivo-deductivo, que parte del análisis de situaciones concretas observadas en el aula para formular interpretaciones y conclusiones sobre la efectividad de las estrategias didácticas.
La población objeto de estudio está compuesta por 26 docentes de la Unidad Educativa Réplicas Nicolás Infante Díaz. Se seleccionó como muestra el total de docentes, garantizando obtención de información relevante y profunda sobre el proceso de enseñanza-aprendizaje.
Para la recolección de datos se empleó como instrumento una encuesta semiestructurada dirigida a los 26 docentes de la unidad educativa, diseñada para identificar el uso de estrategias didácticas orientadas al desarrollo del pensamiento lógico-matemático. La encuesta incluyó preguntas cerradas con una escala de valoración de tres puntos (siempre, a veces, nunca) lo que facilitó el análisis cuantitativo. La investigación permitió recoger información cualitativa fundamentándose en la teoría sociocultural de Vygotsky, que concibe el aprendizaje como un proceso mediado socialmente. Para la evaluación de la variable independiente estrategias didácticas para la enseñanza de matemáticas se tuvieron en cuenta las dimensiones: planificación didáctica, metodologías activas, atención a la diversidad y acompañamiento. En el caso de la variable dependiente desarrollo del pensamiento lógico-matemático se tuvieron en cuenta: razonamiento lógico, competencias cognitivas y motivación hacia las matemáticas.
En análisis de datos de la información obtenida, en las encuestas, fue procesada con Microsoft Excel, lo que permitió identificar tendencias y patrones numéricos.
RESULTADOS
Este estudio, realizado en la Unidad Educativa Réplicas Nicolás Infante Díaz, se analizó la aplicación de estas estrategias mediante una encuesta a los 26 docentes que laboran en el centro.
Al consultar sobre la planificación de actividades específicas para el desarrollo del razonamiento lógico en las clases de matemáticas, como se observa en la figura 1, el 46.15% de los docentes planifica actividades específicas para desarrollar el pensamiento lógico-matemático en sus clases, mientras que el 38.46% lo realiza a veces y el 15.39 % nunca. Este resultado indica 84.61 % de los docentes se preocupa por el desarrollo del pensamiento lógico.
Figura 1. Planificación de actividades para el desarrollo del razonamiento lógico en sus clases de Matemática
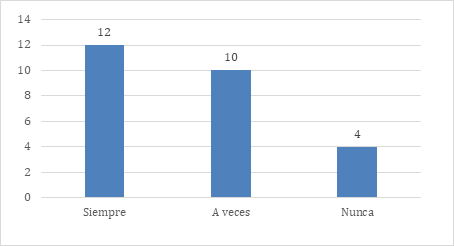
Las respuestas aportadas en este punto sugieren que la mayoría de los docentes mantiene un compromiso con la coherencia curricular y los objetivos pedagógicos institucionales, aunque existe un grupo de profesores a los que le falta responsabilidad en este aspecto por lo cual no se debe de dejar de prestar atención a este aspecto.
La pregunta 2 sobre el uso de juegos o dinámicas que estimulen el pensamiento lógico-matemático, los resultados se muestran en la figura 2.
Figura 2. ¿Utiliza juegos o dinámicas que estimulen el pensamiento lógico en el aula?
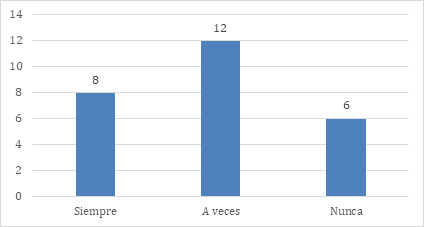
El 30.77% de los encuestados utiliza juego o dinámicas para estimular el pensamiento lógico, incorporando actividades lúdicas que fomenten la participación y el aprendizaje experimental. Sin embargo, el 46.15% presenta un uso limitado de estas estrategias y el 23.08 %, lo que revela una oportunidad de mejora. El fomento de metodologías activas podría elevar la motivación estudiantil y favorecer la adquisición de habilidades cognitivas de manera más atractiva y significativa.
En la figura 3 plasman los resultados a la pregunta sobre la adaptación de las estrategias didácticas a los diferentes estilos y ritmos de aprendizaje.
Figura 3. ¿Adapta las estrategias didácticas a los diferentes estilos y ritmos de aprendizaje?
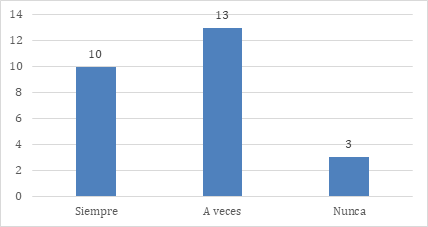
De los encuestados el 38.46 %, se adapta las estrategias didácticas a los diferentes estilos y ritmos de aprendizaje, garantizando la inclusión educativa. El 50 % de los profesores a veces adapta las estrategias. Este dato es positivo, ya que refleja que el cuerpo docente reconoce la diversidad como un elemento central en la enseñanza asegurando que cada estudiante reciba un tratamiento pedagógico acorde a sus características.
Los resultados sobre la aplicación de estrategias de trabajo colaborativo basadas en la interacción social como lo plantea la teoría sociocultural de Vygotsky se muestran en la figura 4.
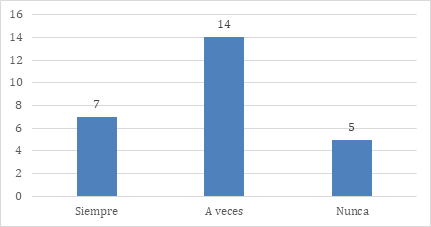
El 26.92 % de los encuestados aplica de manera constante el trabajo colaborativo, siguiendo la teoría sociocultural de Vygotsky, que resalta la interacción social como medio para el aprendizaje. El 53.85 % restante no lo implementa con la misma frecuencia, lo que limita los beneficios de esta metodología, y el 19.23 % nunca la aplica. Este hallazgo evidencia la necesidad de reforzar la formación en estrategias colaborativas para maximizar su impacto en el desarrollo de competencias cognitivas y sociales.
Este panorama pone de manifiesto la importancia de generar espacios de actualización docente que permitan integrar de manera efectiva el trabajo colaborativo en las prácticas educativas, garantizando así que todos los estudiantes se beneficien de sus aportes en el desarrollo académico y social.
Adicionalmente, en la figura 5 se muestran los resultados sobre la pregunta del fomento de la motivación interna y la toma de decisiones en el aprendizaje, como lo plantea la teoría de la autodeterminación de Deci y Ryan.
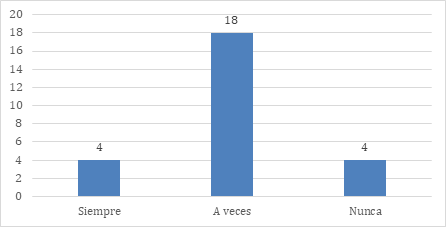
Solo el 15.38 % de los encuestados fomenta la motivación interna y la autonomía en el aprendizaje, conforme a la teoría de la autodeterminación de Deci y Ryan. Estos docentes crean entornos que promueven la iniciativa propia y el interés sostenido. No obstante, el 69.23 % restante no incorpora estas estrategias de manera consistente, lo que podría incidir en niveles más bajos de implicación y desempeño. El 15.38 % nunca las fomenta. Este aspecto requiere intervenciones formativas que incentiven el uso de recursos y dinámicas que fortalezcan la motivación intrínseca.
Las respuestas a la pregunta sobre la relación de los nuevos contenidos con los conocimientos previos de los estudiantes se muestran en la figura 6.
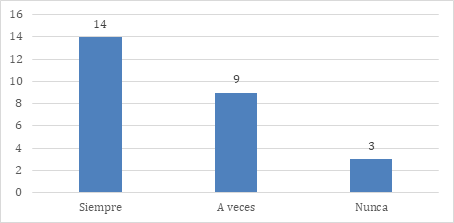
El 53.85 % de los encuestados relaciona los nuevos contenidos con los conocimientos previos de los estudiantes, mientras el 34.62 % lo hace a veces y el 11.54 % nunca. Esta práctica favorece el aprendizaje significativo, al permitir que los estudiantes construyan nuevos conocimientos sobre una base existente. Este resultado se configura como una fortaleza dentro del proceso educativo.
La figura 7 refleja los aspectos correspondientes contextualización de los contenidos matemáticos con ejemplos de la vida cotidiana para facilitar la comprensión de la lógica.
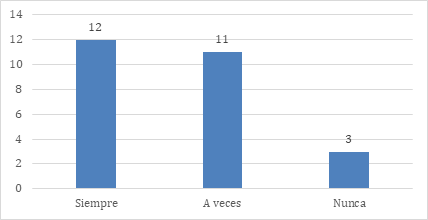
Como se observa en la figura 7, el 46.15 % contextualiza los contenidos matemáticos
con ejemplos de la vida cotidiana, el 42.31 % lo hace a veces y el 11.54 %. Esto contribuye a que los estudiantes comprendan la aplicabilidad de los conceptos abstractos y fortalezcan la conexión entre el aprendizaje escolar y su entorno inmediato.
La utilización de la gamificación se ve reflejada en la figura 8. Sólo el 15.38 % utiliza gamificación de manera constante, mientras que el 50 % no la implementa habitualmente y 34.62 % nunca la utiliza. Esta baja adopción representa una oportunidad para diversificar las metodologías de enseñanza y elevar el interés y la motivación de los estudiantes, incorporando dinámicas de juegos, insignias y retos que fortalezcan el compromiso con el aprendizaje.
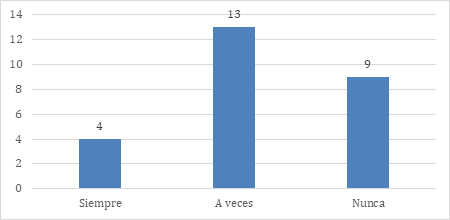
La figura 9 aborda el tema del trabajo colaborativo para resolver problemas de lógica matemática en clase. Como se muestra en la figura 9, el 57.69 % de los encuestados emplea trabajo colaborativo para la resolución de problemas de lógica matemática. El 38.46 %lo aplica a veces y el 3.85 % nunca. Esta práctica potencia la comunicación, el razonamiento lógico y la capacidad para tomar decisiones en grupo, favoreciendo el desarrollo de competencias transversales esenciales para el aprendizaje.
Figura 9. ¿Aplica el trabajo colaborativo para resolver problemas de lógica matemática en clase?
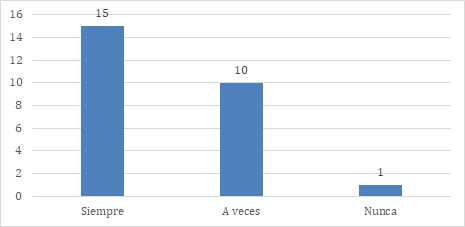
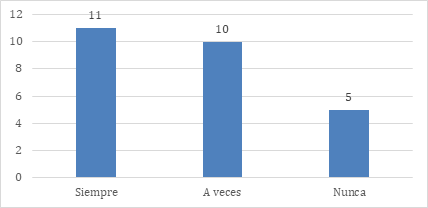
A continuación, la pregunta sobre la retroalimentación a los estudiantes se muestra en la figura 10. De los profesores encuestados el 42.31 % de los encuestados ofrece retroalimentación personalizada durante las actividades de razonamiento lógico. Esta acción fortalece el aprendizaje individual, permitiendo a cada estudiante identificar sus avances y áreas de mejora. El 16,60% que no la aplica de manera habitual representa un margen de mejora que podría impactar positivamente en el rendimiento académico.
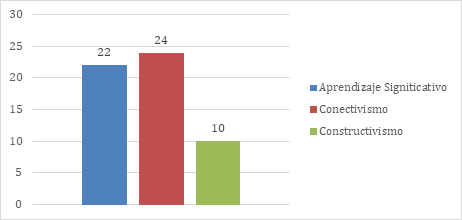
Por último, en la figura 11 se muestra el conocimiento sobre las distintas teorías del aprendizaje. El aprendizaje significativo y el conectivismo son ampliamente conocidos con un 84.62 % y un 92.31 % respectivamente mientras el conocimiento del constructivismo solo obtiene un 38.46 %.
Figura 11. De estas teorías del aprendizaje, marque las que conoce.
Los principales resultados obtenidos en la aplicación de la encuesta se pueden resumir en:
· La mayoría de los docentes planifican actividades específicas para el desarrollo del pensamiento lógico, lo que refleja coherencia entre la intencionalidad pedagógica y la activación del razonamiento lógico en clase.
· El poco uso de juegos y dinámicas y la escasa incorporación de la gamificación revelan una desconexión entre metodologías activas y la motivación intrínseca del estudiantado.
· La inclusión educativa es reconocida pero no plenamente internalizada en la práctica docente, muy pocos docentes adaptan sus estrategias al ritmo y estilos de aprendizaje.
· Una parte de los docentes ofrecen una retroalimentación personalizada durante las actividades, lo que constituye un factor clave para el fortalecimiento de la motivación y guiar la construcción del pensamiento lógico-matemático.
· A pesar de que la mayoría de los docentes declaran conocimiento sobre el aprendizaje significativo y el conectivismo existe una baja implementación de estas teorías en la práctica diaria, mostrando una importante brecha entre el saber y el hacer.
La información recopilada permitió medir las prácticas pedagógicas y su efectividad en el aula. Se destaca la necesidad de implementar estrategias inclusivas que favorezcan el aprendizaje significativo y contribuyan a la calidad educativa.
DISCUSIÓN
Los resultados de esta investigación muestran una tendencia positiva en la aplicación de estrategias didácticas para el fortalecimiento del pensamiento lógico-matemático en estudiantes de Básica Media. El 84.61 % de los docentes encuestados presta interés a planificar actividades específicas y adaptar sus estrategias a los ritmos y estilos de aprendizaje, lo que evidencia un compromiso hacia una enseñanza inclusiva y centrada en el estudiante, en concordancia con lo planteado por Peña (2024) sobre la educación diferenciada y contextualizada. Este enfoque coincide con lo señalado por Nuñez et al. (2020), quienes resaltan que el docente debe promover el análisis, la abstracción y la resolución de problemas adaptándose a las necesidades del grupo.
Asimismo, el uso del trabajo colaborativo y la conexión de los contenidos con situaciones de la vida cotidiana fue valorado positivamente por los encuestados, en línea con los postulados de la teoría sociocultural de Vygotsky y el aprendizaje significativo de Ausubel. Según Velásquez et al. (2023), el trabajo colaborativo fortalece la interacción social y la confianza del estudiante, mientras que Ausubel citado por López de Aguilera & Soler (2021) sostiene que vincular nuevos contenidos con conocimientos previos favorece la comprensión profunda. Estos hallazgos indican que la interacción social y la vinculación con conocimientos previos potencia la comprensión profunda y la aplicación práctica de conceptos matemáticos, contribuyendo al logro del objetivo del estudio.
Sin embargo, se identificó una baja utilización de recursos como la gamificación, que solo es aplicada por el 15.38 % de los encuestados. De acuerdo con Macías & Zambrano (2023) la metodología resulta eficaz para aumentar la motivación y participación en la formación docente para integrar recursos innovadores.
El aprendizaje significativo es muy difundido en la formación docente, altamente utilizado en la planificación curricular. Junto al constructivismo es una de las teorías más reconocidas aplicadas en la práctica educativa del país, pero existe un desconocimiento sobre el conectivismo, por ser una teoría reciente y ligada al aprendizaje digital. Esta brecha, que coincide con lo advertido por Morales et al. (2024) sobre las limitaciones de acceso a oportunidades formativas en ciertos contextos educativos, restringe el potencial de innovación y adaptación a las demandas pedagógicas contemporáneas.
Asimismo, si bien el 83.40 % fomenta la motivación interna y la toma de decisiones, persiste un 16.60 % que no incorpora estos elementos en su práctica. Según la teoría de la autodeterminación de Deci y Ryan, retomada por Donald (2025) y Hernández (2023), la motivación intrínseca se fortalece cuando el estudiante percibe autonomía, mantiene relaciones significativas y desarrolla competencia. La ausencia de estas condiciones reduce el compromiso sostenido y el interés por el aprendizaje, afectando el desarrollo integral en el área de matemática.
En conjunto, es importante fortalecer la formación docente continua, priorizando metodologías activas, la incorporación de teorías actualizadas y el diseño de experiencias educativas participativas, la resolución de problemas y la innovación pedagógica. Se recomienda que las instituciones educativas faciliten el acceso a recursos didácticos, asesorías metodológicas y espacios de innovación que favorezcan una enseñanza de la matemática más pertinente, inclusiva y motivadora.
CONCLUSIONES
Los resultados del presente estudio evidencian una tendencia favorable en la implementación de estrategias didácticas orientadas al desarrollo del pensamiento lógico-matemático en estudiantes de Básica Media, mostrando prácticas docentes centradas en el estudiantes, adaptadas a su ritmo y estilo de aprendizaje, lo que se alinea con los principios de una educación inclusiva contextualizada.
Se destaca la planificación intencionada por parte del profesorado, así como el uso de estrategias como el trabajo colaborativo y la conexión de los contenidos con la vida cotidiana, prácticas que se corresponden con los enfoques teóricos de Ausubel y Vygotsky, contribuyendo al fortalecimiento de habilidades cognitivas superiores, pensamiento crítico y procesos lógicos esenciales para la formación matemática.
No obstante, la baja utilización de estrategias como la gamificación, identificada en un reducido porcentaje del profesorado, revela la necesidad de potenciar la formación docente en metodologías activas. Se constató una desconexión entre la teoría pedagógica contemporánea y la práctica docente, reflejada en el desconocimiento de teorías como el conectivismo, lo que evidencia la importancia de incorporar enfoques actualizados en los programas de formación inicial y continua del profesorado.
Finalmente, en un sector del profesorado se evidencia la ausencia de elementos clave de la motivación intrínseca. De acuerdo con la teoría de la autodeterminación de Deci y Ryan puede afectar la autonomía y el compromiso de los estudiantes. Ante ello, se recomienda fortalecer la capacitación docente en un enfoque que priorice la motivación, la innovación pedagógica y el uso de recursos didácticos actualizados, garantizando así procesos de enseñanza-aprendizaje más efectivos y pertinentes.
REFERENCIAS
Alt, D. (2023). Assessing the benefits of gamification in mathematics for student gameful experience and gaming motivation. Computers & Education, 200, 104806. https://doi.org/10.1016/j.compedu.2023.104806
Bazán Ramírez, A., Márquez Ibarra, L., & Félix López, E. G. G. (2021). Apoyo familiar en el estudio de escolares en un contexto de vulnerabilidad. Revista Educación, 46(1), 16. https://doi.org/10.15517/revedu.v46i1.44903
Cerón Motta, A., & Marreno, N. (2024). Dualidad en el aprendizaje matemático: explorando el enfoque mecánico y el aprendizaje significativo. [Tesis de doctorado, Universidad Pedagógica Experimental Libertador]. Espacio Digital UPEL. https://n9.cl/qnye4
Donald Abi, J. R. (2025). Aproximación a la contribución de la motivación del profesorado de secundaria como factor significativo en la calidad de la enseñanza de ELE en Costa de Marfil. [Tesis Doctoral, Universidad de Granada] DIGIBUG: Repositorio Institucional de la Universidad de Granada https://n9.cl/vwz31q
Hernández Herrera, C. A. (2023). Motivaciones basadas en la autodeterminación para el aprendizaje en universitarios del Instituto Politécnico Nacional de México. TELOS: Revista de Estudios Interdisciplinarios en Ciencias Sociales, 25(2). www.doi.org/10.36390/telos252.08
López de Aguilera, G., & Soler Gallart, M. (2021). Aprendizaje Significativo de Ausubel y Segregación Educativa. Remie Multidisciplinary Journal of Educational Research, 11(1). https://doi.org/10.17583/remie.0.7431
Macías Zambrano, C., & Zambrano Romero, W. (2023). Estrategia Didáctica para uso de la Gamificación- Aprendizaje de Matemáticas en Alumnos de Cuarto Grado. MQR Investigar, 7(3). https://doi.org/10.56048/MQR20225.7.3.2023.1790-1810
Mafarja, N., Mohamad, M. M., Zulnaidi, H., & Fadzil, H. M. (2023). Using of reciprocal teaching to enhance academic achievement: A systematic literature review. Heliyon, 9(7), e18269. https://doi.org/10.1016/j.heliyon.2023.e18269
Morales, J. H., Alvarado, P. A., & Camacho, O. E. (2024). La influencia del nivel socioeconómico de las familias en el rendimiento académico de los estudiantes: un análisis comparativo en entornos urbanos y rurales. Revista LATAM, 5(5), 12. https://doi.org/10.56712/latam.v5i5.2845
Mora Velasco, V. E., López Proaño, N. A., Larrea López, E. N., Pérez Frías, H. L., Aldáz Mejía, O. B., & Criollo Yucailla, R. D. (2024). Influencia de la motivación intrínseca y extrínseca en el proceso de enseñanza-aprendizaje: Una Revisión Sistemática. Magazine de las Ciencias, 9(2), 17. https://doi.org/10.33262/rmc.v9i2.3105
Nerio Delgado, O. G., & Ramírez Puente, T. E. (2024). Ansiedad Matemática. Coloquio internacional de investigación educativa en nivel medio superior, 2(2), 21. http://eprints.uanl.mx/29755/
Núñez Vallejo, L. A., Gallardo Lucas, D. M., Aliaga Pacore, A. A., & Diaz Dumont, J. R. (2020). Estrategias didácticas en el desarrollo del pensamiento crítico en estudiantes de educación básica. Eleuthera, 22(2). https://doi.org/10.17151/eleu.2020.22.2.3
Peña Garmendia, T. N. (2024). El docente y los tipos de estrategias didácticas para la enseñanza de las matemáticas. Revista Ciencias Sociales y Humanas, 7(2). https://doi.org/10.47606/ACVEN/PH0330
Rodríguez Rodríguez, D. (2023). Análisis de la influencia de la familia en el rendimiento académico en Educación Secundaria Obligatoria mediante árboles de decisión. Revista Electrónica de Investigación Psicoeducativa, 21(61), 22. https://doi.org/10.25115/ejrep.v21i61.8267
Ruiz Peralta, K. A., & Reyes Acaro, M. J. (2025). Estrategias didácticas para el proceso de enseñanza aprendizaje de matemáticas en educación secundaria. Uniandes Episteme, 12(2). https://doi.org/10.61154/rue.v12i2.3699
Taufikurrahman, T., Budiyono, B., & Slamet, I. (2021). Development of mathematics module based on meaningful learning. AIP Conference Proceedings, 2330, 040032. https://doi.org/10.1063/5.0043239
Valero Rodrigo, N., & González Fernández, J. L. (2021). Análisis comparativo entre la enseñanza tradicional matemática y el método ABN en Educación Infantil. Universidad Valladolid Revistas, 9(1), 22. https://doi.org/10.24197/edmain.1.2020.40-61
Velásquez Álava, W. L., Vivero Cedeño, A. D., Rivas Posligua, W. O., Farfán Polanco, T. Y., & López Vera, J. R. (2023). Aprendizaje colaborativo en la enseñanza de matemática. Revista Científica Arbitrada Multidisciplinaria PENTACIENCIAS, 5(6), 21. https://doi.org/10.59169/pentaciencias.v5i6.842